NOVIEMBRE
CLASE N°5
Fecha: 09-11-2016
EJERCICIO
En una empresa financiera, los empleados disponen de computadoras portátiles de distintas marcas, un resumen de números de máquinas, de acuerdo a su respectiva marca se presenta en el siguiente cuadro
Marca
|
Número de respuestas (ni)
|
Fi(%)
|
Ángulo
|
Toshiba T
|
135
|
41.4
|
149
|
Dell D
|
76
|
23.3
|
84
|
Hp HP
|
53
|
16.3
|
58
|
Lenovo L
|
43
|
13.2
|
48
|
No sabe NS
|
19
|
5.8
|
21
|
X= Marca de las computadoras portátiles (Cualitativas)
Mo= Marca Toshiba
DIAGRAMA DE BARRAS
Este diagrama no sirve para variables cuantitativas.
Título: Frecuencias relativas de las marcas de computadoras portátiles.
Descripción
El gráfico N° 1 representa las frecuencias relativas de las marcas de computadoras portátiles en una empresa comercial.
Interpretación
En el gráfico N°1 Se evidencia que la marca Toshiba presenta una alta relatividad, mientras que la opción no sabe existe un bajo porcentaje.
DIAGRAMA CIRCULAR O SECTORES
360 100%
X 41.4%
DATOS AGRUPADOS EN INTERVALOS O CLASES
1.- Decidir el número de clases o intervalos.
K= 1+3.3log(n)
Donde:
K: # de clases o intervalos
n: # de observaciones
2.- Calcular la longitud de la clase (A)
A= Xmax- Xmin / K
3.- Construir las clases o intervalos
4.- Calcular las columnas de la tabla de frecuencia
DIAGRAMA DE TALLOS DE HOJAS
Es una técnica estadística para representar un conjunto de datos. Cada valor numérico se divide en dos partes. El o los dígitos principales forman el tallo están colocados a lo largo del eje vertical, y las hojas de cada observación a lo largo del eje horizontal.
Este diagrama es usado cuando hay un número no muy pequeño de datos.
HISTOGRAMA
Gráfico que coloca:
En el eje OX: los intervalos o clases de variables
En el eje OY: la frecuencia absoluta o relativa
POLÍGONO DE FRECUENCIA
OJIVA
Una ojiva se utiliza para representar la frecuencia acumulada. Similar al Polígono de frecuencias , se forma o se construye uniendo los puntos más altos de cada columna pero de un histograma que representa las Frecuencias Acumuladas.
CLASE N°6
Fecha: 11-11-2016
En esta clase se realizaron ejercicios aplicando Datos agrupados en intervalos
EJERCICIO
EJERCICIOS VARIOS
CLASE N°7
Fecha: 16-11-2016
En esta clase realizamos la actividad CORAZÓN , hicimos sus gráficas, las describimos e interpretamos, al igual que calculamos medias, media, desviación estándar.
Su realización la podemos ver en TALLER 1
CLASE N°8
Fecha: 18-11-2016
MUESTRAS BIVARIABLES
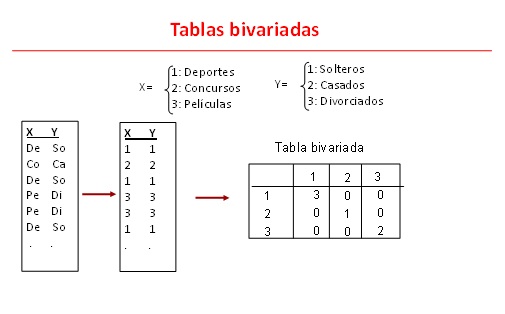
Dos variables para una misma muestra
Tenemos tres pasos a seguir:
i) Identificar las variables
ii)Realizar un diagrama de dispersión y=f(x)

iii) Analizar la correlación
i) Identificar las variables
ii)Realizar un diagrama de dispersión y=f(x)
iii) Analizar la correlación
CORRELACIÓN
Relación que presentan las variables involucradas, existen cuatro tipos:
COVARIANZA MUESTRAL
Sean X1, X2, ......Xn e Y1, Y2,....Yn dos muestras aleatorias independientes de observaciones de X e Y respectivamente. La covarianza poblacional se estima como:
Sean
Sean
La covarianza es una medida de la correlación entre las variables.
Si Sxy es mayor que 0 entonces la tendencia es lineal positiva
Si Sxy es menor que 0 entonces la tendencia es lineal negativa
COEFICIENTE DE CORRELACIÓN (r)
Valor de r
|
X y Y
|
Cercano a 1
Cercano a -1
Cercano a 0
|
Tiene
correlación lineal positiva fuerte.
Tiene
correlación lineal negativa fuerte.
Tiene
correlación lineal muy débil o no están correlaciones linealmente.
|
MATRIZ DE VARIANZA - COVARIANZA
MATRIZ DE CORRELACIÓN
CLASE N°9
Fecha: 19-11-2016
En esta clase rendimos la primera prueba bimestral.
Su solución la podemos observar en: TAREA 4 Corrección de la Prueba
CLASE Nº 10
FECHA: 23 de Noviembre del 2016
FECHA: 23 de Noviembre del 2016
PROBABILIDAD
Medida cuantitativa de que tan probable es que ocurra un evento.
Ideas Principales
- Al conjunto de todos los posibles resultados de un experimento se le llama espacio muestral.
- Un subconjunto de un espacio muestral se denomina evento.
- Se dice que un evento ocurrió si el resultado del experimento es alguno de los resultados en el evento. Por ejemplo, si un dado cae en el número 2, habrán ocurrido los eventos {2, 4, 6} y {1, 2, 3}, junto con cualquier otro evento que contenga el resultado “2”.
Combinación de eventos
Con frecuencia se construyen eventos mediante la combinación de eventos más sencillos. Debido a que aquéllos son subconjuntos de espacios muestrales, es usual emplear la notación de conjuntos para describir los eventos construidos de esta forma. A continuación se repasará la notación necesaria.
Los eventos se pueden mostrar gráficamente con los diagramas de Venn. Muestra los eventos A unión B, A intersección B y B intersección A complemento.
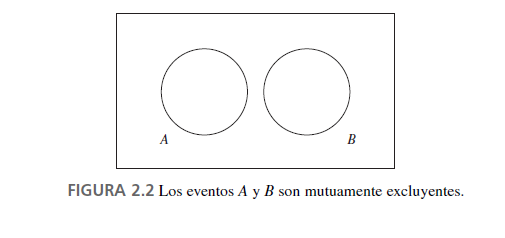
Eventos mutuamente excluyentes
Se dice que los eventos A y B son mutuamente excluyentes si no tienen resultados en común.
De forma más general, se dice que una colección de eventos A1, A2, . . . , An es mutuamente excluyente si dos de ellos no tienen resultados en común.
Dado un experimento y cualquier evento A:
- La expresión P(A) denota la probabilidad de que ocurra el evento A.
- P(A) constituye la proporción de veces que se presenta el evento A en el tiempo, si es que el experimento se realizara una y otra vez.
Axiomas de la probabilidad
El tema de la probabilidad se basa en tres reglas de sentido común, conocidas como axiomas.
Éstas son:
EJEMPLO
El objetivo de una prueba de tiro consiste de un blanco rodeado por dos anillos concéntricos. Se dispara un proyectil hacia el objetivo. La probabilidad de que pegue en el blanco es de 0.10, la de que atine en el anillo interior es de 0.25 y la de que acierte en el anillo exterior es de 0.45. ¿Cuál es la probabilidad de que el proyectil haga blanco en el objetivo? ¿Cuál es la probabilidad de que no pegue en este último?
Solución
Pegar en el blanco, acertar en el anillo interior y atinar en el anillo exterior son eventos mutuamente excluyentes, ya que es imposible que más de uno de éstos ocurra a la vez.
P(pega en el objetivo)= P(blanco) P(anillo interior) P(anillo exterior)
= 0.10 0.25 0.45
=0.80
Ahora se puede calcular la probabilidad de que el proyectil no pegue en el objetivo
P(no pega en el objetivo) = 1 - P(pega en el objetivo)
=1 - 0.80
= 0.20
DIAGRAMA DE ÁRBOL
Referencia:
Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006
Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006
CLASE Nº 11
Fecha: 25 de Noviembre del 2016
Fecha: 25 de Noviembre del 2016
MÉTODOS DE CONTEO
Si una operación se puede realizar de n maneras y si para cada una de esas n maneras se puede realizar una segunda operación de n2 maneras, entonces el número total de maneras en que se realizan las dos operaciones es:
n1*n2
EJEMPLO 1
Cierto tipo de automóvil se encuentra disponible en tres colores: rojo, azul o verde, y puede tener un motor grande o pequeño. ¿De cuántas maneras puede un comprador elegir un automóvil?

Tamaño del motor: n1= 2
Color del automovil: n2 =3
n1 * n2= (2) (3) = 6
Número total de maneras de elegir = 6
EJEMPLO 2
Cuando se hace un pedido de cierto tipo de computadora, hay tres elecciones de disco duro, cuatro de la cantidad de memoria, dos de la tarjeta de video y tres de monitor. ¿En cuántas maneras se puede solicitar una computadora?
Solución
El número total es (3)(4)(2)(3) 72.
PERMUTACIONES
- Es un ordenamiento de un conjunto de n elementos.
- El número de permutaciones de n elementos es n!
- El número de permutaciones de n elementos es n!
n! = n(n-1)(n-2)....2(1)
0!=1
1!=1
Ejemplo 1:
¿ Cual es el número de permutaciones de arreglos con las letras: A, B, C?
Si A, B, C ------ n=3------ =3!
=6 [ ABC, BAC, BCA, ACB, CAB, CBA ]
PERMUTACIONES DE k ELEMENTOS
El numero de permutaciones de k elementos de un total de n elementos.

Ejemplo:
Un grupo de 10 personas puede elegir a su directiva: presidente, secretario, tesorero. Todos pueden ser elegidos, pero una persona no puede tener mas de un cargo. De cuantas maneras diferentes puede realizarse la elección.
k=3 3P10 = (10!)/(10-3)!= 720
n=10
Otra forma:
10(9)(8)= 720
Casos particulares:
- Se puede presentar que el arreglo sea circular, entonces el número de permutaciones es (n-1)!
- Se puede presentar que el arreglo sea circular, entonces el número de permutaciones es (n-1)!
Ejemplo
De cuántas maneras se pueden colocar 5 personas en una mesa.
n=5 (4)(3)(2)(1)= 24
De 24 formas se puede colocar a las 5 personas.
Si se tiene elementos repetidos entonces el número de permutaciones es:
Ejemplo
En una caja hay 3 botellas de vino tinto y 2 de vino blanco. Las botellas de cada uno de los dos tipos de vino tienen la misma marca y forma. ¿De cuántas formas diferentes puede colocarse en una hilera de 5 botellas?
n=5
n1=3 #total de maneras= 5!/3!*2!
n2=2 =10
Otro ejemplo AQUÍ
COMBINACIONES
Son arreglos de k elementos elegidos de un grupo de n elementos. En estos arreglos el orden no importa.
En estos arreglos el orden no importa.
Para más información y observación de ejemplos clic AQUÍ
CLASE Nº 12
Fecha: 30 de Noviembre del 2016
En esta clase realizamos ciertos ejercicios relacionados con el tema que vimos anteriormente.
Experimento: Selección de una persona de una habitación
P(A) = 11/18 ; P(C) = 9/18 ; P(A∩C) = 5/18
b) P(AUC) = 11/18 + 9/18 - 5/18= 15/18
P(Ac) = 7/11 ; P(Bc) = 11/18 ; P(Ac∩ Bc) = 0
c) P(AcUBc) = 7/18 +11/18 =1
Diagrama de árbol:

PROBABILIDAD CONDICIONAL
Diagramas de Venn para ilustrar la idea de la probabilidad condicional.
En una caja hay 3 botellas de vino tinto y 2 de vino blanco. Las botellas de cada uno de los dos tipos de vino tienen la misma marca y forma. ¿De cuántas formas diferentes puede colocarse en una hilera de 5 botellas?
n=5
n1=3 #total de maneras= 5!/3!*2!
n2=2 =10
Otro ejemplo AQUÍ
COMBINACIONES
Son arreglos de k elementos elegidos de un grupo de n elementos. En estos arreglos el orden no importa.
En estos arreglos el orden no importa.
Para más información y observación de ejemplos clic AQUÍ
CLASE Nº 12
Fecha: 30 de Noviembre del 2016
En esta clase realizamos ciertos ejercicios relacionados con el tema que vimos anteriormente.
Ejercicio 1
En una habitación se encuentra el siguiente grupo de personas: 5 hombres mayores de 21, 4 menores de 21, 6 mujeres mayores de 21, 3 mujeres menores de 21. Se elige una persona al azar y se definen los siguientes sucesos:
a: La persona es mayor de 21
b: La persona es menor de 21
c: La persona es hombre
d: La persona es mujer
Evaluar las siguientes probabilidades:
a) P(BUD)
b) P(AUC)
c) P(AcUBc)
Experimento: Selección de una persona de una habitación
A
|
B
|
||
C
|
5
|
4
|
9
|
D
|
6
|
3
|
9
|
11
|
7
|
18
|
P(B) = 7/18 ; P(D) = 9/18 ; P(B∩D) = 3/18
a) P(BUD) = P(B) + P(D) - P(B∩D)
= 7/18 + 9/18 - 3/18 = 13/18P(A) = 11/18 ; P(C) = 9/18 ; P(A∩C) = 5/18
b) P(AUC) = 11/18 + 9/18 - 5/18= 15/18
P(Ac) = 7/11 ; P(Bc) = 11/18 ; P(Ac∩ Bc) = 0
c) P(AcUBc) = 7/18 +11/18 =1
Diagrama de árbol:

PROBABILIDAD CONDICIONAL
Diagramas de Venn para ilustrar la idea de la probabilidad condicional.
Ejemplo
En un proceso que fabrica latas de aluminio, la probabilidad de que una lata tenga alguna fisura
en su costado es de 0.02, la de que otra la tenga en la tapa es de 0.03 y de que una más presente
una fisura en el costado y en la tapa es de 0.01. ¿Cuál es la probabilidad de que una lata tenga
una fisura en el costado, dado que tiene una fisura en la tapa?
Solución
Se tiene que P(fisura en la tapa)= 0.03 y que P(fisura en el costado y fisura en la tapa)=
0.01,
P(fisura en el costado | fisura en la tapa)= P(fisura en el costado y fisura en la tapa)/ P(fisura tapa)
= 0.01/0.03
=0.33
Otro ejemplo lo podemos ver AQUÍ
Referencia:
Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006
Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006

























No hay comentarios:
Publicar un comentario