CLASE Nº 13
Fecha: 2-12-2016
En esta clase rendimos la EVALUACIÓN 2
CLASE Nº 14
Fecha: 7-12-2016
En esta clase lo primero que se realizo fue la corrección de dos de los ejercicios que se encontraban en la evaluación 2
1) Los artículos provenientes de una línea de producción se clasifican en defectuosos (D) y no defectuosos (N). Se observan los artículos y se anota su condición. Este proceso se continúa hasta que se produzcan dos artículos defectuosos consecutivos o se hayan verificado cuatro artículos, lo que ocurra primero. Describa el espacio muestral para este experimento.
Solución:
S={DD, NDD, DNDD, DNDN, DNND, DNNN, NDND, NDNN, NNDD, NNDN, NNND, NNNN}
2) Sean los A,B y C tres eventos asociados con un experimento. Exprese las siguientes proposiciones verbales en notación de conjuntos.
a) al menos uno de los eventos ocurre.
b)exactamente uno de los eventos ocurre.
c)exactamente dos de los eventos ocurre.
d)no ocurre mas de dos eventos simultáneamente
a) al menos uno de los eventos ocurre.
b)exactamente uno de los eventos ocurre.
c)exactamente dos de los eventos ocurre.
d)no ocurre mas de dos eventos simultáneamente

3) Se realizo una encuesta en Cuenca para determinar el numero de lectores de El Mercurio y La Hora. Los resultados fueron que el 32% lee El Mercurio, el 27% lee La Hora y el 8% lee los dos.
a. Coloque la información en una tabla de doble entrada.
B
|
BC
|
||
A
|
0.08
|
0.24
|
0.32
|
AC
|
0.19
|
0.49
|
0.68
|
0.27
|
0.73
|
1.0
|
b. Coloque la información en un Diagrama de árbol
c. Si se selecciona al azar un lector de La Hora ¿Cual es la probabilidad de que lea El Mercurio?
P(A/B)=P(A∩B)/P(B)= 0.08/0.27
d. Si se ha seleccionado un lector de El Mercurio ¿Cual es la probabilidad de que no lea La Hora?
P(B^C/A)=P(A∩B^C)/P(B^C)=0.24/0.32
EVENTOS INDEPENDIENTES

Si A y B son independientes, entonces los siguientes pares de eventos son también independientes:
A
y BC, AC y B y AC y BC. La prueba de este hecho se deja como ejercicio.
El concepto de independencia se puede ampliar para más de dos eventos:


REGLA MULTIPLICATIVA DE LA PROBABILIDAD
Sena A y B elementos no nulos cualquiera de S entonces
Definición: Regla multiplicativa de la probabilidad.
Ejemplo
En una caja hay 10 baterías de las cuales 4 están en buen estado. Se extraen al azar dos baterías sin devolverlas a la caja. Calcule la probabilidad que:
a) Ambas baterías existen en buen estado
b) Solamente una batería este en buen estado
c) Al menos una batería este en buen estado
d) Ninguna batería este en buen estado
REGLA MULTIPLICATIVA DE LA PROBABILIDAD PUEDE EXTENDERSE A MÁS EVENTOS
Definición: Regla multiplicativa de Probabilidad por tres eventos
Ejemplo
Dos jugadores de fútbol realizaron un disparo cada uno. Se conoce que la probabilidad de éxito del primero es 0.7 mientras que la probabilidad de éxito del segundo jugador es 0.6.
a) Ambos jugadores tengan éxito
b) Ninguno tenga éxito
c) Al menos uno tenga éxito
Solución:
P(A)= 0.7
P(B)= 0.6
a) P(A∩B)=
P(A) P(B) = 0.7*0.6= 0.42
b) P(Ac∩
Bc)=P(Ac)(Bc) = 0.3*0.4= 0.12
c) P(A⋃C) = P(A)+P(B)-P(A∩B)=
0.7+0.6-0.42=0.88
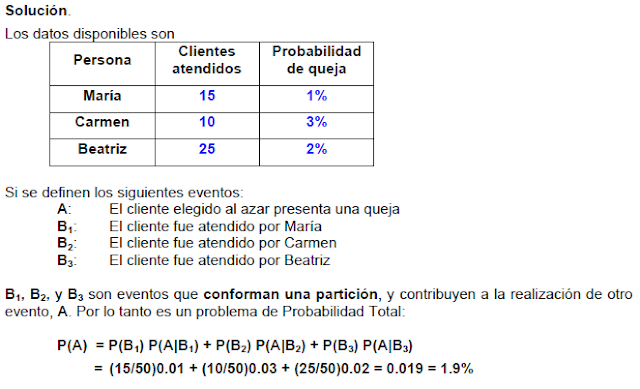
PROBABILIDAD TOTAL
Ejemplo
Una empresa tiene 3 personas para atender a sus clientes María, Carmen y Beatriz. Se disponen de un registro histórico de porcentaje de quejas de los clientes atendidos por estas tres personas el 1%, 3%, 2% respectivamente. Cierto día acudieron 50 clientes a la empresa de los cuales 15 fueron atendidos por María, 10 por Carmen y 25 por Beatriz.
Referencia:
Luis Rodriguez. (2007). Probabilidad y estadistica basica para ingenieros. Quito: ESPOL.
CLASE N° 15
Fecha: 10-12-2016
1.- En un juego de 40 se reparten 5 cartas al azar a cada jugada
a partir de un mato de 40 cartas. ¿Cuál es la probabilidad de que jugador
tenga:
a)Un dos, un tres, un cuatro, un cinco del mismo palo
b) 4 cartas del mismo
palo
c)Una ronda (3 cartas
iguales)
Solución
a) P(B)= P(A cualquier palo)·P(2palo igual A)·P(3igual palo)·P(4igual
palo)·P(5igual palo)
P(B)= (4/40) ·
(1/39) · (1/38) · (1/37) · (1/36) = 5.06*10^-8
b) C: 4 cartas del mismo palo. {A, 2, 3, 4, 5, 6, 7, 8, 9}
P(C)= (4/40) ·
(9/39) · (8/38) · (7/37) = 2.29*10^-4
c) D: Ronda.
P(D)= P(1carta) · P(2da carta= #) · P(3ra carta=#)
P(D)= (1/40) ·
(3/39) · (2/38) = 1.01*10^-4
2) Una empresa tiene 2 tiendas distribuidas una en el norte
y otra en el sur. De los clientes se sabe que el 30% solo compra en la tienda
norte, el 50% solo en la tienda sur, el 10% compra indistintamente en las 2
tiendas. Y el 10% de los consumidores no compran en ninguna de ellas.
A= El cliente compra en la tienda norte
B= El cliente compra en la tienda sur
Calcule las siguientes probabilidades
a) P(A)
b) P(AUB)
c) P(Bc)
d) P(A∩B)
e) P(A/B)
f) P(Ac∩Bc)
g) P(A∩B)^c
h) P(AUB^c)
A
|
AC
|
||
B
|
10
|
50
|
60
|
BC
|
30
|
10
|
40
|
40
|
60
|
100
|
a) P(A)= P(AUB) + P(AUB^c)=0.1+0.3=0.4
b) P(AUB)= P(A)+P(B)-P(A∩B)= 0.4+0.6-0.1=0.9
c) P(Bc)= 0.9
d) P(A∩B)=0.1
e) P(A/B)= P(A∩B)/P(B) =0.1/0.6
f) P(Ac∩Bc)= 0.1
g) P(A∩B)^c = P(AUB)=0.9
h) P(AUB^c)= P(A)+P(B^c)-P(AUB^c) =0.4+0.4-0.3=0.5
3) En la intersección de una autopista, los automoviles pueden girar a la derecha D o a la izquierda I. Desde un puesto de observación se registra el sentido de la maniobra de los tres primeros vehiculos.
a) Cual es el espacio muestral del experimento
b) Sea A el suceso a lo mas de uno de los coches gira a la derecha. Sea B el suceso todos los coches giran en la misma dirección. Sea C el suceso exactamente uno de los coches gira a la derecha. ¿Qué relación existe entre los sucesos B y C?
c) Enunciar y hallar los elementos de los sucesos: Bc , BUC, A∩B, Ac∩Bc

a) S={DDD, DDI, DID, DII, IDD, IDI, IID, III}
b) A={III, IID, IDI, DII}
B={III, DDD}
C={IID, IDI, DII}
c) BC=(IID, IDI, DII, DDI, IDD,DID)
BUC=(DDD, III, IID, IDI, DII)
A ∩B=( III)
AC ∩BC= (AUB)C
AUB=( III,DDD,IID,IDI,DII)
(AUB)C= (DDI,IDD,DID)
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL.
SEGUNDO BIMESTRE
CLASE N°1
Fecha: 14-12-2016
VARIABLES ALEATORIAS DISCRETAS
Las variables aleatorias establecen correspondencia de los espacios muestral al conjunto de los números reales.
Definición: Variable Aleatoria
EJEMPLO
Tabule la correspondencia que establece la variable aleatoria x:
S= ( ( c,c,c ) , ( c,c,s ) , ( c,s,c ) , ( s,c,c ) , ( c,s,s ) , ( s,c,s ) , ( s,s,c ) , ( s,s,s ))
X= Variable aleatoria ( número de sellos que se obtienen)
x= 0,1,2,3
e (
elementos de S)
|
X (valor
de X)
|
( c, c ,c )
(c, c , s )
( c, s, c )
( s, c, c )
( c, s , s )
( s ,c ,s)
( s, s ,c )
( s, s, s )
|
0
1
1
1
2
2
2
3
|
Donde X= S
rg de x= ( 0, 1, 2, 3)
Las variables aleatorias pueden representarse con letras mayúsculas X , Y ...
Para un mismo espacio muestral S pueden definirse muchas variables aleatorias,
Y: diferencia entre el número de caras y el número de sellos.
Su rango sería: rg Y= { -3, -1, 1, 3 }
Z: el número de caras al cubo, más el doble del número de sellos.
Su rango sería: rg Z= { 5, 6, 10, 27 }
Según el tipo de correspondencia establecida, las variables aleatorias puedes ser discretas o continuas.
EJEMPLO
En un experimento se lanza repetidamente una moneda. Determine el rango y el tipo de variable aleatoria discreta siguiente:
S= ( ( s ) , ( c,s ), ( c,c,s ) , ( c,c,c,s ) , .....)) posibles resultados
rg X= ( 1,2,3,4, ... )
X es una variable aleatoria discreta.
DISTRIBUCIÓN DE PROBABILIDAD DE UNA VARIABLE ALEATORIA DISCRETA
Probabilidad de una variable aleatoria discreta
Sea X= variable aleatoria discreta
Entonces P(X=x) representa la probabilidad que la variable X tome el valor x.
La correspondencia que define P(X=x) es una función y se denomina Distribución de Probabilidad de la variable aleatoria X. Esta correspondencia puede definirse formalmente y ser designada con la notación f:
Distribución de probabilidad de una variable aleatoria discreta X
f es una función de probabilidad, por lo tanto su rango esta en el intervalo (0,1)
Propiedades de la distribución de probabilidad de una variable aleatoria discreta.
EJEMPLO:
FUNCIÓN DE DISTRIBUCIÓN DE PROBABILIDAD
La gráfica es asimétrica.
HISTOGRAMA DE PROBABILIDAD
Cuando los valores posibles de
una variable aleatoria discreta están espaciados uniformemente, la función de
masa de probabilidad se puede representar por medio de un histograma, con
rectángulos centrados en los valores posibles de la variable aleatoria. El área
de un rectángulo centrado en un valor x es igual a P(X x). Este histograma se llama un histograma de
probabilidad, ya que las áreas representan probabilidades.
EJEMPLO
Sea X una variable aleatoria discreta cuya distribución de
probabilidad está dada por:
(1/14)
x2, x= 0, 1, 2, 3
P(X=2)= (1/14) (2)^2= 2/7
X
|
f (x)
|
0
1
2
3
|
0
1/14
4/14
3/14
|
DISTRIBUCIÓN DE PROBABILIDAD ACUMULADA DE UNA VARIABLE ALEATORIA DISCRETA
- Distribución de probabilidad acumulada de la variable aleatoria x
EJEMPLO
Encuentre la distribución de probabilidad acumulada para el ejemplo de las tres monedas.
La distribución acumulada puede graficarse:
PROPIEDADES DE LA DISTRIBUCIÓN ACUMULADA PARA VARIABLES ALEATORIAS DISCRETAS
El dominio de F es el conjunto de los números reales, por lo tanto es válido evaluar F(x) para cualquier valor real de x.
CLASE N°2
Fecha: 16-12-2016
MEDIA Y VARIANZA DE LAS VARIABLES ALEATORIAS DISCRETAS
Definición
Sea x una variable aleatoria discreta con función de densidad de probabilidad p(x)=f(x) = p(X=x), la media de x esta dada por:
MEDIA O ESPERANZA

Propiedades de la media o esperanza

Un ejemplo calor lo podemos observar AQUÍ
Desviación Estándar

Varianza

Propiedades de la varianza

Para reforzar nuestros conocimientos podemos ver los siguientes ejemplos :
VARIABLES ALEATORIAS CONTINUAS
Definición
Una variable aleatoria es continua si sus probabilidades están dadas por áreas bajo una curva. La curva se llama función de densidad de probabilidad ´por la V.A
La función de densidad de probabilidad también es llamada distribución de probabilidad.
Debe cumplirse:
- También se dice que X es continua si P(X=x)=0 (Probabilidad puntual).
- Si F^f son funciones de distribución y de densidad de la variable aleatoria continua, se cumple:
P(a< x<b) = F(a) - F(b)
Para más información clic AQUÍ
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL.
CLASE N°3
Fecha: 21-12-2016
EJEMPLOS
1.- Suponga que el tiempo de atención de cada cliente en una estación de servicio es una variable aleatoria continua con la siguiente función de densidad de probabilidad:
a) Verificar si cumple las
propiedades de una función de densidad
1.- 0≤ x≤1
2≤x+2≤3
4≤ 2(x+2)≤6
4/5≤2/5(x+2)≤6/5
4/5≤ F(x) ≤6/5
2.-
Representación gráfica
b) Calcule la probabilidad que el tiempo de atención este entre 15 y 30 minutos
FUNCIÓN DE DISTRIBUCIÓN
Definición: Función de distribución
Definición: Propiedades de la función de distribución
La propiedad 3 es útil para calcular los valores de probabilidad de la variable x.
EJEMPLO
Encuentre la función de distribución para el ejemplo anterior
Respuesta
Esta es una función cuyo dominio es el conjunto de los número reales
Gráfico de la función de distribución
Use la función de distribución para calcular P( 1/4 < X < 1/2 )
Respuesta
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL.
























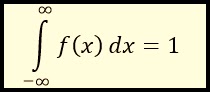










El primer ejercicio para el espacio muestral falta NDD
ResponderEliminar